Next: Evaluierung und Simulation
Up: Erweiterungen zu Guaranteed Percentage
Previous: Bestimmung der Anteile
Inhalt
Eine weitere Möglichkeit, Threads mit kurzer Deadline einzuplanen, besteht darin, für jeden Thread das Intervall mit anzugeben, in dem er seinen Anteil bekommen muß. Damit ist festgelegt, wann ihm Rechenzeit entzogen werden darf, und wann das zu Verletzungen von Deadlines führen würde.
Gegeben seien (n-1) Threads
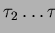 mit den Raten
mit den Raten 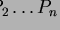 in den Intervallen
in den Intervallen 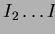 .
Dazu kommt ein Thread
.
Dazu kommt ein Thread 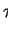 mit D1<T1, für den wir zunächst annehmen, I1 sei kürzer als alle anderen Intervalle. Er werde nur einmal innerhalb des längsten Intervalls aufgerufen. Ist
mit D1<T1, für den wir zunächst annehmen, I1 sei kürzer als alle anderen Intervalle. Er werde nur einmal innerhalb des längsten Intervalls aufgerufen. Ist
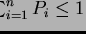 ,
so kann der Thread auf jeden Fall angenommen werden. Anderenfalls muß man anderen Threads im System kurzfristig Rechenzeit entziehen, die man ihnen später in ihrem Intervall wieder zurückgibt.
,
so kann der Thread auf jeden Fall angenommen werden. Anderenfalls muß man anderen Threads im System kurzfristig Rechenzeit entziehen, die man ihnen später in ihrem Intervall wieder zurückgibt.
Abbildung:
Intervalle und Rechenzeitzuweisung für n=3
|
|
Abbildung 2.12 zeigt ein Beispiel für n=3. Der zusätzliche Bedarf von 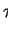 ,
der den anderen Threads entzogen werden muß, ist
,
der den anderen Threads entzogen werden muß, ist
also der Teil, um den die Summe der Pi 100% überschreitet.
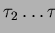 seien oBdA nach aufsteigender Intervallänge sortiert. Dann kann jedem Thread
seien oBdA nach aufsteigender Intervallänge sortiert. Dann kann jedem Thread
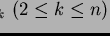 der Anteil
der Anteil
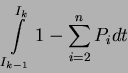 |
(2) |
innerhalb des Intervalls Ik-1 entzogen werden. Formel 2.2 beschreibt die Prozessorleistung, die  zurückerhalten kann, wenn er für den Rest seines Intervalls die gesamte Restleistung des Prozessors erhält.
zurückerhalten kann, wenn er für den Rest seines Intervalls die gesamte Restleistung des Prozessors erhält.
Maximal kann den Threads
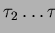 also
also
entzogen werden. Damit ist auch der Fall abgedeckt, daß I1 nicht das kürzeste Intervall ist. Weiterhin bedeutet das insbesondere auch, das man die zusätzlich benötigte Rechenleistung direkt von dem Thread mit dem längsten Intervall abziehen kann.
Der neue Thread 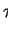 kann also genau dann angenommen werden, wenn er nicht mehr zusätzliche Rechenleistung braucht, als dem System maximal entzogen werden kann:
kann also genau dann angenommen werden, wenn er nicht mehr zusätzliche Rechenleistung braucht, als dem System maximal entzogen werden kann:
Da 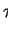 nur innerhalb seines Intervalls ausgeführt wird, also P1=0 für t>I1 gilt, folgt:
nur innerhalb seines Intervalls ausgeführt wird, also P1=0 für t>I1 gilt, folgt:
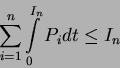 |
(3) |
Daraus ergibt sich folgender Scheduling-Algorithmus: Der neue Thread wird angenommen, falls die Ungleichung 2.3 erfüllt ist, sonst abgelehnt. Wenn 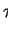 aktiv ist (in dem Intervall I1), wird dem Thread
aktiv ist (in dem Intervall I1), wird dem Thread 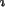 mit dem längsten Intervall die Rechenleistung entzogen, die
mit dem längsten Intervall die Rechenleistung entzogen, die 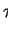 zusätzlich benötigt. In der restlichen Zeit bekommt
zusätzlich benötigt. In der restlichen Zeit bekommt 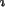 die gesamte Restleistung des Prozessors zugeschlagen. Damit ist auch der Fall abgedeckt, dass
die gesamte Restleistung des Prozessors zugeschlagen. Damit ist auch der Fall abgedeckt, dass 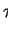 erst am Ende des Intervalls In aktiv wird.
erst am Ende des Intervalls In aktiv wird.




Next: Evaluierung und Simulation
Up: Erweiterungen zu Guaranteed Percentage
Previous: Bestimmung der Anteile
Inhalt
Alexander Schulz
2000-06-18
![]() mit den Raten
mit den Raten ![]() in den Intervallen
in den Intervallen ![]() .
Dazu kommt ein Thread
.
Dazu kommt ein Thread ![]() mit D1<T1, für den wir zunächst annehmen, I1 sei kürzer als alle anderen Intervalle. Er werde nur einmal innerhalb des längsten Intervalls aufgerufen. Ist
mit D1<T1, für den wir zunächst annehmen, I1 sei kürzer als alle anderen Intervalle. Er werde nur einmal innerhalb des längsten Intervalls aufgerufen. Ist
![]() ,
so kann der Thread auf jeden Fall angenommen werden. Anderenfalls muß man anderen Threads im System kurzfristig Rechenzeit entziehen, die man ihnen später in ihrem Intervall wieder zurückgibt.
,
so kann der Thread auf jeden Fall angenommen werden. Anderenfalls muß man anderen Threads im System kurzfristig Rechenzeit entziehen, die man ihnen später in ihrem Intervall wieder zurückgibt.
![]() ,
der den anderen Threads entzogen werden muß, ist
,
der den anderen Threads entzogen werden muß, ist
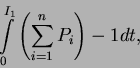
![]() also
also
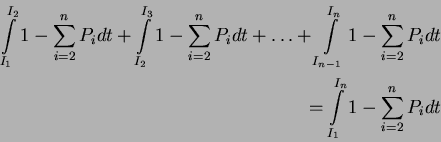
![]() kann also genau dann angenommen werden, wenn er nicht mehr zusätzliche Rechenleistung braucht, als dem System maximal entzogen werden kann:
kann also genau dann angenommen werden, wenn er nicht mehr zusätzliche Rechenleistung braucht, als dem System maximal entzogen werden kann: